
Background
Lesson
Home > Archive > For teachers > Negatives (Math) > Lesson
![]()
![]()
Students will be able to:
- Explain the difference between a number and an integer.
- Describe the history of negative numbers.
- Define positive and negative integers.
- Analyze the following mathematical operations: addition, subtraction, multiplication, and division of positive and negative integers.
- Create algorithms for the integer operations using manipulatives and SpicyNodes.
Level: Grade 7
![]()
- Computer lab
- 12 inch rulers
- Two measuring tapes
- Positive and negative sign counters in two different colors
NOTE: You can be creative in making positive and negatives sign counters as manipulatives. Cost-effective manipulatives include cardboard pieces; pipe cleaners; and plastic tags upon which the positive and negative signs can be written with permanent markers.
Time needed: 8-10 class periods of 60-minutes
![]()
Computer lab
![]()
![]()
- Introduce the concept of integers by asking the students to name some numbers, which leads to defining whole numbers.
- Provide students with a handout containing integers, decimal numbers, and fractions. Ask them to sort them out. Using SpicyNodes is an option at this point.
- Introduce the concept of negative integers using the example of a hotel that has the lobby on the first floor, a garage one level below the lobby, a swimming pool two levels below the lobby, and sleeping rooms on floors 2-7, above the lobby. Using the lobby as the point of reference, students can visualize that the elevator is going up to the room or down to the pool or the garage.
| Sample Table | |
|---|---|
| Rooms | 4th floor +3 |
| Rooms | 3rd floor +2 |
| Rooms | 2nd floor +1 |
| Lobby | 1st floor (street level) 0 |
| Garage | Basement (1 level below the lobby) -1 |
| Pool | Below the garage -2 |
- Provide an historical context (The History of Negative Numbers) and examples of the use of negative integers in real life.
- Demonstrate the concept of positive and negative integers. Explain the conventions such as going east (positive) and west (negative) using rulers with a center point as the origin. Other demonstrations could include using two measuring tapes placed east and west with a reference point as the origin and asking a student to walk on one side (east) and then the opposite (west). Then, ask students to draw a number line with 0 as the reference point (origin).
For concrete example, students could think of the falling music CD sales and the rising sales of digital music. An online marketing research site, eMarketer, estimated a drop in U.S. recorded music spending from about $11 billion in 2006 to $10 billion in 2008 and $9 billion in 2011. It is estimated that, in 2011, recorded music spending will be $2 billion less (i.e., changes by -$2 billion) from 2006. Three years from 2008, it is estimated that spending will decrease by about $1 billion (i.e., changes by - $1 billion).
Introduce the idea that negative numbers may represent change such as a drop in temperature or drop in prices, etc.
Multidisciplinary Connections - World History and Geography: Ask students to read the historical examples of negative numbers and the related geographical locations. Students can create a SpicyNodes presentation with this information. Prompts could include: At those points of time in history, what was happening in the West? How did people in the East contribute to mathematics?
![]()
![]()
- Introduce the concept of absolute value as the number of units (or the distance) a number is from 0, the reference point.
- Guide the students to recognize that (a) if no sign is written in front of an integer, it is positive; for example 4-5 can be expressed as +4-5; (b) the inverse of a negative integer is a positive integer. First, demonstrate the addition and subtraction of positive integers. Next, demonstrate the addition and subtraction of negative integers. Then, demonstrate the addition of the positive and negative integers, explaining how the combination of a + and - will cancel out. Introduce the idea of a negative integer as an inverse of a positive integer. Help students recall the concept of subtraction. Here is an example:
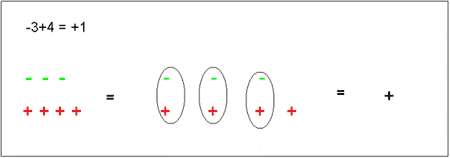
- Introduce the rules for addition and subtraction using concrete examples such as money, with income representing the positive integer and debt representing negative integer. Adding two incomes will result in greater income. Adding two debts will result in more debt. Adding positive and negative integers is like finding out if income is higher than debt or viceversa.
- Provide a work sheet for addition and subtraction. Here is a template. Ask students to use the positive and negative sign counters to find the answers.
| 3 + 4 = | -3 + 7= |
| -3-4 = | -7 +3 = |
| -6+4 = | -3-7 = |
- Based on the discussion of rules of addition and subtraction, as well as the work sheet, guide students to come up with rules.
- Using the concept of absolute value, guide students to come up with rules of addition and subtraction:
![]()
| Integer addition and subtraction | Rule |
|---|---|
| Integers of the same sign (++ or - -) | Add the absolute value. Give the result the same sign. -7-4 = -11 |
| Integers of opposite sign (+ -) | Take their absolute values. Subtract the smaller from the larger. The result will have the sign of the larger integer. -11+3 = -11+(+3) = -8 |
![]()
- Review the concepts of multiplication. It is crucial to connect the relationship between multiplication and addition or subtraction. This can be accomplished using manipulatives. Relate the multiplication with negative integers to real life scenarios. Here are some examples:
- Consider 1 gallon of water in a can. Addition of ice cubes lowers the temperature of water. The change in temperature (final temperature after the addition of ice cubes - initial temperature before the addition of ice cubes) will be negative. Removing ice cube from water will eventually increase the temperature, especially if you remove several or all the ice cubes. Therefore, the temperature of water will rise and the change in temperature (final temperature after removing the ice cubes - initial temperature with ice cubes present) will be positive.»>
- Multiplication of two negative integers resulting in a positive product can be related to removing ice cubes from a 1 gallon water can resulting in a rise of temperature of water. One can think of this analogy as follows: removing ice cubes is equivalent to multiplying a negative integer with -1. One ice cube is equivalent to (-1) since it results in lowering the temperature. Removing one ice cube one time results in a positive change in temperature which is similar to - (-1) = -1 times (-1) which is +1 . Removing three ice cubes at one time is equivalent to - (-3) which is -1 times (-3) = +3. Students can perform experiment to connect this abstract idea to concrete experience. They will learn that negative numbers may represent change such as drop in water temperature and and also connect the multiplication of two negative integers to real life.»>
- A simplified but concrete example is the increase of gas prices by 2012, while the prices of old cars that consume more gas per mile will fall sharply. Assuming that gas prices increase by $3 per year on average, five years from now, the gas price could increase by 5 times $4 which is $20. Then, ask the students to compare this with the prices of items that may lose value with time, such as an old car. For example, if the price of an old car decreases by about $500 (i.e changes by - $500) per year, the price of an old car 5 years from now would be $2500 less because 5 times (-$500) is $-2500.»>
- Using the manipulatives of positive and negative signs, ask students to start with a negative 1 (-1) and create a multiplication table using the repeated addition process. For example, −1 times 2 is (-1) + (-1), and −1 times 3 is adding (-1) 3 times, i.e., +(-1) + (-1) + (-1). (-1) times -3 is removing (-1) 3 times, i.e., -(-1) -(-1)-(-1) = +3. Also explain that -(-1) is the inverse or opposite of (-1) which is +1.
- Provide students with a worksheet that contains multiplication of numbers with the same and opposite signs (++, +- and –). Help them understand how the product of two negative integers is a positive integer.
- Guide students to come up with rules for multiplication by asking them which general rule might they might create based on their answers to the problems in the worksheet.
![]()
| Multiplying Integers | Rule |
|---|---|
| Integers of the same Positive sign (++) | Product is the product of their absolute values. Give the result the same sign. 7 x 4 = 28 |
| Integers of same negative sign (- -) | Product is the product of their absolute values. Give the result a positive sign because negative of a negative integer is positive. -3 x -4 = +12 |
| Integers of opposite sign (+ -) | Product is the product of their absolute values. Give the result a negative sign. «br/> -3 x 4 = -12 |
Multidisciplinary Connections - Science: Students can perform experiments to observe the drop and rise in water temperature with the addition and removal of ice cubes.
Multidisciplinary Connections - Language Arts: Students may explore the history of double negatives usage in English language and relate the multiplication of two negative integers to a positive product.
![]()
- Review the concepts of division with reference to real life situations, like dividing debt among four business partners.
- Provide a worksheet to students that contains division of numbers with same and opposite signs (++, +- and –).
- Guide students to devise rules for Division by asking them which general rule they might create based on their answers to the problems in the worksheet.
![]()
| Division of Integers | Rule |
|---|---|
| Integers of the same Positive sign (++) | Perform the division of the absolute values. 8 /4 = 2 ; -8/-4 = 2 |
| Integers of opposite sign (+ -) | Perform the division using the absolute values. Give the result a negative sign. 8/-4 = -2; -8/4 = -2 |
![]()
- Orientation: Demonstrate the working of SpicyNodes to the class.
- In all the above activities students can use the SpicyNodes to recognize the interrelationships among the arithmetic operations and rules; provide examples, etc. that enables them to "organize and consolidate their mathematical thinking" and "recognize and use connections among mathematical ideas" thus meeting the NCTM standards. Yet another advantage of this process is that students will do ongoing informal self-assessment and engage in cooperative leaning by learning from one another since they need to provide relevant information. Here is a simple example:
| Spicy Nodes template coming up soon |
|---|
![]()
Divide the class into half and assign the following two projects to each half of the class. Divide each half into small groups of 3 to 4 students while balancing the gender and abilities of students.
After completing the project, students groups in each half of the class will do peer assessment and compare their SpicyNode maps. All the groups will then present their Nodemaps in the class. Students may also give these presentations to other classes and families on science and math nights, math clubs, etc.
![]()
Visit the world facts and figures web site: Elevation Extremes by Country. Find out the highest and lowest elevations of at least 10 countries from all the seven continents across the world. Record your findings as a number line indicating the elevations.
![]()
Visit the web site that maps the world time zones: World Time Zone Resources. Record the time zones of the countries as a number line that indicates the local times, expressing them, as they appear on the site, as hours away from Greenwich Mean Time.
What is the role of negative integers in the elevations/time zones data? How are they useful? Create a SpicyNode map to present your findings while explaining the addition, subtraction and multiplication of integers using the elevations/time zones data. What else did you find out about elevations and time zones? You can enter it in the SpicyNode map.
| Spicy Nodes template coming up soon |
|---|


