Site archive. SpicyNodes was active 2005-2018.

Home > Archive > Developers/reference > Background > Browsing Networks

While browsing hierarchies is a system that inevitably follows subordination, an alternative approach employs browsing of elemental structures without taking into account the superiority or inferiority of their interrelated components. As this kind of browsing does not necessarily relate to a perception of verticality, it tends to be open-ended, involving simple jumping among connected topics. These notional hubs, with their mutual linkages considered, form a pattern of a “network” type.

When compared with trees and hierarchies, networks (also known as graphs because of their underlying mathematical theory) represent a more fundamental structure that can be used to describe relations between pieces of information. Networks are useful when relationships are complex or disordered. Examples of a myriad of objects and topics interconnected in large, extensive networks with inner relations are: cities and the roads connecting them; seas and rivers; computers and other communication devices in the global Web; landline phone lines; and dynamic mobile, mostly wireless, networks.

People use such structures mentally everyday, such as when thinking about consequences of actions, social networks among friends, business colleagues, and ideas or philosophical theories. Words in a thesaurus, for instance, connect a word with its synonyms and antonyms. In an art museum, a network could lead the viewer to distantly related works, as: Les Demoiselles d’Avignon, 1907 > Cubism > Art Deco > Art Nouveau > Hector Guimard > Paris Métro entrances. The network, often visualized as a web, represents relationships.

Still, this useful approach has limitations. Anyone who has tried searching through a particular topic or engaging in general educational reading has experienced the “lost-in-space” syndrome. It manifests itself most often in general browsing as the sensation of losing context or looping through the same topics. Its occurrence is aggravated by factors such as an author using different or unexpected terms for naming a concept.

In contrast to hierarchies, where the ever-narrowing set of categories that must be traversed before the sought-after information is found can feel like a labyrinth walk, the browsing of networks feels like boundless, unfettered exploration. In a thesaurus, for example, a reader can jump among related words, or in an encyclopedia, among related articles. On a broader level, the Internet is based on using hyperlinks to link together billions of web pages. Links can be overly focused (e.g., “Read more about the brown spotted owl’s habitat”), or more mercurial (e.g., “Check out this list of cool new artists”).

A recent development in network browsing involves browsing by preference, the popularity of which has been powered by the growth of social networking sites such as LinkedIn and MySpace. In these models, users search for a type of information (for example, another user who lives nearby, or who has similar taste in music, or who has a useful skill set) rather than for a specific, known item. This partially resolves the problem of users needing to know specific keywords in order to retrieve useful information.

For example, a small business owner might search LinkedIn for a developer who can build a useful software application for his business. The businessman may not be familiar with the names of the technologies involved, such as PHP, MySQL, LAMP, and so forth. In a standard search model, such as Google, this would be a handicap, as he would be unaware of some of the key search terms. By searching using the terms “database” or “database programmer,” some relevant results might be returned, but his search would be less efficient than if he had known the proper keywords. In contrast, a preference-based search allows him to interrogate a network by a process of narrowing down a list of potential providers by skill set, area, pay requirements, and so forth.

Ironically, even though they are more natural structures than hierarchies, networks are not always intuitive. Although the human brain could be said to represent a large network of connected neurons, it is not very adept at processing and memorizing such networks. Networks should be used with caution, because although they represent many related concepts well, they do not directly map to our real world experiences of navigating, and they can be more confusing than hierarchies. Whereas hierarchies are like trees, networks can become like science-fiction portals, jumping from node to node in hyperspace, and it is easy to get lost.

The idea of using network structures for organizing information strips the browsing process of the notion of order and subordination. This feature makes it possible for the pursuit of information to become naturalistic and organic. Movement is not achieved by adhering only to the paths imposed by a hierarchy. In fact, motion is no longer perceived in horizontal and vertical planes but is rather thought of as directional. Such simplification renders browsing comfortable and intuitive, although it runs the risk of leading the user outside of his or her realm of interest.

Because there are no navigation rules and proscriptions, networks enable browsing to approximate the evolutionary process. Reaching destinations and achieving goals do not materialize in an algorithmic manner, but are instead arrived at on an empirical basis. The user accumulates knowledge in the process, which helps him or her find information that is even more relevant. Further, the activity itself stimulates creativity and facilitates insight.

Ongoing research in the field of networks has led to the appearance and increasing utilization of structures that possess another vital organic attribute: the ability to learn and mature through regulatory feedback. So-called neural networks can recognize, remember, and prioritize valid patterns by mimicking the way in which the human brain operates. Neural nets are considered especially useful in environments where inexact, approximate solutions are sought. The development of neural nets is closely tied with the study of artificial intelligence.

Cyberspace

Networks as information-organizing structures and navigation tools have been an integral and substantial part of computing over the past decades. The omnipresent global “network of networks,” the Internet, serves as the perfect example of how such a construction can represent a virtual space.

Shortly after the novelist William Gibson coined the term “cyberspace” more than 20 years ago, the notion became synonymous with the then-emerging Internet. This metaphor has been widely and ubiquitously used ever since. In its current shape and complexity, the global network has modeled virtual space and brought it closer to an entire virtual world populated by digital species and diversified by virtual communities.

Because of the uncontrolled growth of information on the Internet, navigation and the means of reaching desired information have become increasingly problematic. The lack of direct correspondence between virtual space and actual reality, as noted by Piazzalunga and Barretto (2005), further exacerbates this issue.

Swiss mathematician Leonhard Euler (1707-1783) represented concepts using nodes and the connections between them, laying the foundation for graph theory. Euler sought to solve the problem known as Bridges of Koenigsberg (today, the Russian’s Kaliningrad). The river of Koenigsberg separates into two branches, forming an island. At the time, the citizenry built seven bridges to cross the river, which were favorite places for Sunday afternoon strolls (Figure 13, left). The issue arose as to whether it was possible to find a route that would allow all seven bridges to be crossed without crossing any of them more than once.

Euler managed to prove that no such route was possible. He recognized that the exact forms of the landmasses, river, and bridges was irrelevant to the problem, and he reduced it to the diagram at right in Figure 13, showing four nodes representing the parks, connected by seven arcs, representing the bridges. From this simplification of the problem, he worked out a number of principles relevant to systems of interconnected nodes, providing the tools to later describe and solve diverse problems as the “shortest path problem,” the “traveling salesman problem,” the “Chinese postman problem,” and so on.

The layouts are conceptual, and nodes can be positioned many ways. The art lies in devising layouts that look appealing and informative (3). Early layouts were arranged in a radial manner when drawing free trees, or trees without a specified root (5).

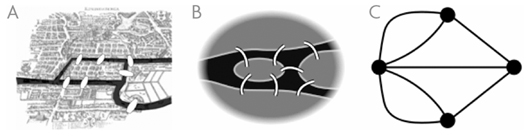
Figure 13. Graph theory was developed in response to the historical Bridges of Koenigsberg problem. A. View of the bridges. B. View of only the river and bridges. C. Simplified representation.

Today, we know that the graph network is a set of objects called “nodes” or “points” of any kind connected by lines, named “links” or “edges.” They are called “edges” because in a simple visualization (Figure 14), the nodes appear as vertexes and the links appear as edges of polygons. The links usually constitute a supplementary set, except when there is a graphical representation of the graph.

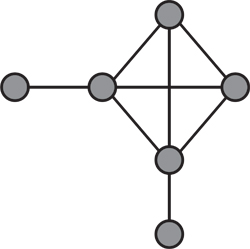
Figure 14. Depiction of a graph as a set of objects connected by lines.

Graphs may be directed or undirected. A directed graph forces users to move from node to node in a particular sequence, with their choices determining which sequence they take. An undirected graph allows freedom of movement. The Internet, for instance, would be modeled as a directed graph, since the user chooses to click on a link to move on to the next page. However, with a browser’s back button functionality, the Internet becomes an undirected graph. Because every node (web site) is itself another tree or graph, the Internet is, in essence, a graph of graphs.

The information architecture of a website can be an example of a directed graph, in which each page is a node and the hyperlinks between pages are the edges. It is not always possible to travel back and forth along the edges. For example, the payment sequence of an e-commerce site may direct a user through a series of pages to achieve his or her goal. He or she may not go back along the route followed except by stepping outside the directed graph of the site’s architecture and forcing a return by pressing the “back” button on the web browsers.

A road map is a classic example of an undirected graph. If we consider New York, Chicago, and Washington D.C. as nodes on a graph and the roads between them edges, then clearly we can travel back and forth along those edges as we please. The only occasions for which maps cease to be undirected graphs is on a much smaller scale, perhaps in a town or city that has a system of one-way streets. In such a situation, navigation from place to place in the city would be described by a directed graph, because the route taken to get to A from B might not be permitted as a route to get from B to A.

Graphs are differentiated by orientation, limitation of the number of edges, additional attributes of the nodes or links, coherence, and so on. There are five properties that differentiate undirected graphs, or those in which links are not oriented, from trees:

Undirected graphs lack hierarchy. The links are undirected; there is no parent/child relationship between nodes as in a tree.

Undirected graphs are not necessarily interconnected. In contrast, a tree is, by definition, interconnected, as there is a route between any given pair of nodes. But in an undirected graph (or, in concrete terms, the Internet as a whole) such a route is not required. A web site or intranet, for instance, could contain no external hyperlinks and not be linked to or accessible from any other web site or network.

Undirected graphs can have an unlimited number of links. In contrast, every node of a tree, except the root, is the target/subject of exactly one link. In undirected graphs, this count ranges from zero to infinity. This requirement splits the nodes into levels of distance from the root of the tree. Because there is only one entry point to a node, and every edge leads along only one route, the distance from the root (usually expressed by the number of links contained in the route between the root and the node) is constant. The accepted level or depth of the node in a tree is its distance from the root.

Undirected graphs have no “home” node. A tree has one source node: the root. In undirected graphs, all nodes are equivalent.

Loops are possible in undirected graphs. A tree does not contain any loops since every node is the target/subject of exactly one link.

These differences make undirected graphs much more powerful and flexible when representing the structure of complex and large relationships, but more cumbersome for individuals - especially those who do not have immediate access to a computer. Still, graphs remain a very useful and flexible tool with a broad range of applications. For example, radial trees are very effective in presenting cyclic or cross-level complex relationships and for representing knowledge in a way that users can instinctively understand.