Site archive. SpicyNodes was active 2005-2018.

Home > Archive > Developers/reference > Background > Browsing Hierarchies

For millennia, humanity has stored information to pass it on to later generations or to use for reference at a later time. As language developed, knowledge representation was communicated verbally and stored mentally. With the evolution of the written word, information was stored more reliably and permanently. Over time, writing led to the education of more and larger groups of people — exponentially increasing, for a time, the repository of human knowledge. Before long, handwritten texts became inadequate for the number of people needing to access information.

Eventually, the existence of a huge quantity of printed books led to the challenge of effective search and retrieval. This needle-in-a-haystack problem becomes more acute as the metaphorical haystack increases in size. Consider an example of searching for a particular book in a library.

Any search process is analogous to looking for a book in a bookcase with randomly arranged books. Represented mathematically, if someone wants to search through 100 books, the value “N” would be 100. At this stage, the person looks through the books one by one (a linear search algorithm). Searching among N topics, the person would have to look through half the books (N/2 accesses) on average, which is manageable if N is a small number. In a small bookcase, the person would look through fifty books on average (100/2) before finding the book being sought.

From a historical perspective, once the human knowledge base grew exponentially, due to a power function of writers, content descriptions, areas of knowledge, and so forth, the number of topics quickly made linear search impractical. In other words, N/2 is impractically large. This led to the development of tree-like structures, such as a book classification system in a library or a table of contents that organized the information fragments in a book. By dividing topics into a cascading set of categories and subcategories, it became possible for people to quickly find the topics they wanted.

The number of topics increases exponentially with the number of levels of subcategories. For example, if each category has ten subcategories, then ten levels can encompass 10 billion topics. Coincidentally, this is the maximum capacity of the well-known International Standard Book Number (ISBN) that is used as a unique identifier for books. In contrast, if someone browses a tree of information, narrowing the topic each time the person passes a level, the process is inverted, and the number of items the person needs to examine is a logarithm. In mathematical terms, assuming the tree is balanced, the user faced with 50 items searches log2 (N)/2, or an average of just ten iterations of five item searches.

Hierarchical structures are useful because most knowledge is interconnected. In language, we often reference the relationship, using words such as “is” (a rose blossom is a flower), “has” (a flower has fragrance) and “inherits” (a son inherits his mother’s eyes). We also acknowledge hierarchical relationships using designations such as “superior-inferior” when referring to military or corporate positions. Likewise, we classify people and objects by “membership” of a type, class, family, kind, and so forth. In information dissemination, radial trees give a visual representation of the relationships that language usually conveys.

Advances in formalizing knowledge led to the concepts of class and classification as a means of categorizing objects and notions by groups of observed properties. The systematic approach of classification played a significant role in the formation of the knowledge core of virtually every science subject. Categorization has contributed considerably to usability in non-scientific environments as well. In an art museum, a hierarchy could lead the viewer to a particular artwork, as: Painting > European Art > 20th Century > Cubism > Picasso > Les Demoiselles d’Avignon, 1907

When areas of knowledge were not easily represented or categorized in linear, verbal structures such as sentences and paragraphs, visual representations began to appear. As a result, graphics, sketches, and diagrams were employed to categorize non-linear information. Hierarchy diagrams, genealogy trees, and biology classification schemes, for example, demonstrated related networks of information more naturally. Many of these classification systems were so extensive that one or even several printed pages were insufficient to visualize them fully. That in turn led to some visual representations becoming cumbersome.

A primary example is the classification system introduced in 1753 by the Swedish botanist Carolus Linnaeus (Linnaeus, 1735), who systematically categorized living things and represented them in the Tree of Life (Figure 3). He grouped all organisms according to a two-part name (a “binomial”). The first part of the name is the generic grouping, usually called the “genus.” The second part is the specific grouping - or “species.” Classification systems of that type have a pronounced hierarchical structure, where nodes represent the objects, concepts, and facts that are divided by levels, and are interconnected by relationships between the successor-predecessor, class member, type, species, and so forth. Today, scientists continue to use Linnaeus’ basic system, but with many additional levels of hierarchical organization.

Figure 3. The Tree of Life, Carolus Linnaeus’ systematic categorization of living things.

Hierarchical structure is most appropriate when, moving from level to level, the same kind of relationship is depicted, such as “parent-child” or “genus-species.” While precisely how the mind stores related information is unknown, at a conscious level it seems that we often use a tree-like hierarchy. We are born into genealogies tracing back to common ancestors, which would indicate a possible common method of storing and formatting knowledge and information about the world around us. Indeed, the evolution of life itself involves the differentiation and specialization of one species to the next, from single-celled organisms to the plethora of unique species we see today. That our knowledge system is very dynamic is evidenced by the fact that relationships within a hierarchical structure are strictly of one kind, yet we understand the rich set of possible relationships between structures or within different views of same structure. For this reason, information units have to possess flexible structures and adhere to the nesting principle of Russian nesting dolls – that is, the recursive insertion of one informational unit into another. Any information unit should be able to be nested in the content of any other, and from any unit it should be possible to distinguish one or more composing units. In other words, an opportunity must exist that allows for the arbitrary settlement of relationships between information units such as “part-whole” or “object-class.” Again, a tree-like structure is a prime candidate for organization because, by definition, it meets that requirement.

Hierarchies provide a virtual space for users to manipulate and find files. The use of tree-like structures to represent information has become commonplace, being utilized for everything from library classification systems to web sites. Computer users are very familiar with hierarchies because computer operating systems use the metaphor of storing “files” in “folders” or “directories,” which can be nested. When trees became inadequate to completely describe information, references and hyperlinks were introduced, whether inside a document as a table of contents, or as references to external documents, information, or knowledge.

As previously mentioned, a prerequisite for representing information in a hierarchical structure is that the kind of relationships is consistent across the tree. In the real world though, relationships are more complex and require a variety of structures to fully represent the information. In genealogy, for example, relationships such as “brother” or “brother-in-law” need to be depicted. Similarly, academic papers often have multi-tiered tables of contents so that the authors can address complex subjects by dividing them into more manageable subtopics.

There are a number of tools that can be used to depict these complex relationships. A complementary tree that presents only the additional relationships can be developed, or references and hyperlinks can be used across the same tree to supplement the relationships depicted in the main hierarchy of information. By definition, the latter example actually breaks the hierarchical structure because it becomes a non-hierarchical network or graph.

Today, we see an increasing number of tree-like structures that organize information, such as photographs, mind maps, site maps, interactive visualizations, dynamic visuals (animations), and even physical objects. They all improve the transfer of knowledge by using computer- and non-computer-based complementary visuals. Animations, for example, have the potential to enhance our understanding of systems that change over time.

Tree representations are often the most appropriate and natural tool to use when categorizing and understanding information. However, there are cases where tree structures reinforce the notion of hierarchy, and others that take a different approach.

As simple hierarchical structures, trees normally comprise a set of nodes with directional relations. The direction indicates parent and children nodes. However, linear tree layouts become cluttered when the nodes are too numerous to be visualized in a single view, as often happens with medium- and large-sized web sites that employ sitemaps. Clutter can be reduced by selectively choosing sub-branches of the tree to view, as explored by Heer and Card’s DOI Trees, and Grosjean et al.’s SpaceTree. (7)(14)

Early attempts to chart the contemporary universe of knowledge in detail employed hierarchical tree-like structures, such as Ephraim Chambers’ seminal 18th century Cyclopaedia (1728). The author described the work as “An universal dictionary of arts and sciences: containing the definitions of the terms, and accounts of the things signify’d thereby, in the several arts, both liberal and mechanical, and the several sciences, human and divine…. The whole intended as a course of antient and modern learning.” Chambers’ Cyclopaedia was the inspiration for the landmark Encyclopédie (Diderot & d’Alembert, 1751), edited by Denis Diderot and Jean le Rond d’Alembert. Figure 5 depicts the “Figurative system of human knowledge,” from the Encyclopédie, which organized knowledge into three main branches: memory, reason, and imagination.

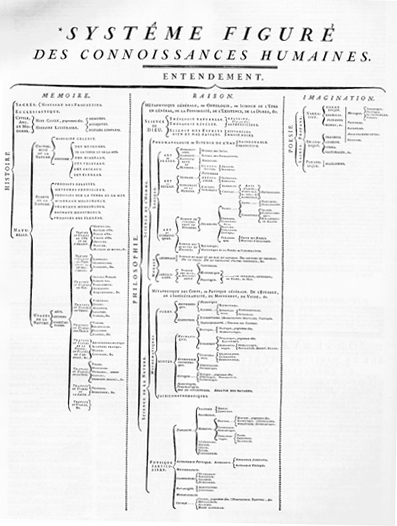
Figure 5. Figurative system of human knowledge, from Diderot’s 1751 “systéme figure” for the Encyclopédie.

Circular tree models are useful in displaying a hierarchy of any size within the finite area of a circle. Focus is acquired by enlarging the portion of the space currently in view. The number of outer leaf nodes increases exponentially in large hierarchical structures. Yee, et al. introduced advances in making radial map exploration more intuitive, including improved layouts, constrained animations when changing focus, and visualization of both hierarchical and network data (19).

Hyperbolic radial trees can display large numbers of nodes and offer smooth transitions when the focus is changed by translating a structure from a hyperbolic plane to Euclidian space (10)(8). In hyperbolic space (12), the circumference of a circle is always exponentially more than 2πr and the angle polar coordinate in a hyperspace can have a range greater than 2π. With hyperbolic space, many items can fit into the periphery and the view can be warped in real time, moving distortion through the field of view. However, the periphery is excessively warped.

Rather than geometrical calculations, force-based or force-directed algorithms can also create appealing layouts with minimal overlapping and relatively consistent distances between nodes. These algorithms generally assign forces among the set of edges and the set of nodes, as if the edges were springs. Nodes push and pull on each other iteratively as the system nears an equilibrium state.

There are several toolkits that provide programmers access to the leading algorithms and techniques from the last few decades, as well as platforms for devising new visualizations. For example, the “Prefuse toolkit” (prefuse.org) supports several types of visualization and interaction techniques and back-end features such as data modeling and searching.